
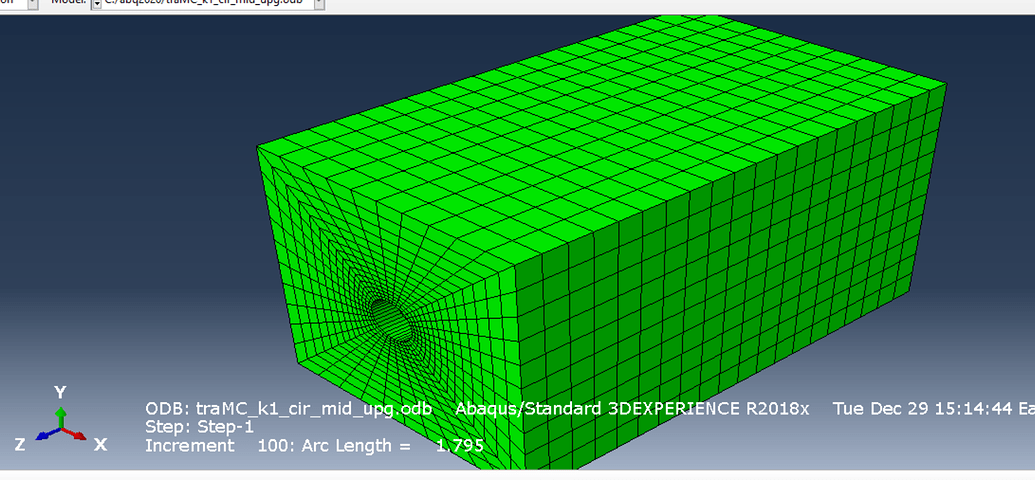
Clockwise from upper left: linear-elastic, mean value coordinate, weighted condition number, and radial basis function smoothing.
Unlike the other three methods, there is no edge crossing in the WCN mesh.įigure 1: Examples of interpolation schemes applied to an HO mesh adjacent to a wavy wall. A two-dimensional version of the weighted condition number (WCN) smoothing approach described in this article produced the result shown in the lower right of Figure 1 (the white mesh). One particularly challenging case was the wavy wall illustrated in Figure 1 that was meshed with HO triangles of degree 4. Each method was successful in most of the cases attempted. Previous mesh curving research performed at Pointwise explored the LE, RBF, and MVC methods in two dimensions. Interpolation of the boundary deformation onto the interior can employ simple weighted interpolation using nearest surface points, radial basis functions (RBF) to define interior point motion, mean value coordinates (MVC), or other bases. Linear-elastic (LE) smoothing treats the mesh elements as a collection of deformable viscoelastic solids with stiffness of the elements imposed through specification of Young's Modulus and Poisson's Ratio. This definition is important because the terms order and degree are often used synonymously.)Ĭurving of HO meshes is typically accomplished using deformation techniques that employ smoothing or interpolation of the boundary deformation into the mesh's interior. Therefore, a linear mesh has degree 1 and order 2, a quadratic mesh has degree 2 and order 3, etc.
#Fieldview unstructured paraview plus
(Note: For the purpose of characterizing an HO mesh, its order is equal to its polynomial degree plus one. Therefore, some type of mesh smoothing or improvement is often required before these meshes can be used in high-order (HO) FEM simulations. The high aspect ratio mesh cells near no-slip boundaries can become inverted or suffer other quality problems when their linear edges are updated to curved (higher polynomial order) shapes for boundary conformance. Degree elevation is not usually a problem except for elements near highly curved geometric boundaries. P-refinement requires elevating the polynomial degree of linear meshes. This increased accuracy can be obtained by adding points to the mesh (termed H-refinement) or by increasing the polynomial degree of the basis function assumed for the solution within each element (termed P-refinement). The initial bandwidth and profile reported from renumberMesh (OpenFOAM v2006) were 7 and 300, respectively.Finite-element methods (FEM) for computational fluid dynamics (CFD) simulations are increasing in popularity for many reasons, one of which is the relative ease with which more accurate solutions can be obtained. Our first case is a simple structured mesh, as shown in Figure 1. This numbering does not necessarily result in a low bandwidth or profile matrix upon export. Pointwise stores the mesh internally in a format and numbering that is efficient for mesh generation. By default, OpenFOAM uses Cuthill-Mckee but also offers reverse Cuthill-McKee, Sloan, Zoltan, Structured, Spring and Random (not for use). OpenFOAM has an application called renumberMesh that reduces the bandwidth and profile of the coefficient matrices by renumbering the cell label list. Most CFD solvers either renumber the mesh without user intervention or provide an application for the user to renumber the mesh manually. There are many sparse matrix renumbering strategies, with the most commonly used in CFD being the Cuthill-McKee. The goal of mesh renumbering is to reduce the matrix bandwidth and profile.
This locates the leftmost nonzero element in each row. The bandwidth of the matrix is defined byĪnother important quantity is the matrix profile. Clustering of all the nonzero elements near the diagonal makes “A” a banded matrix. These are solved using iterative or direct methods. Implicit discretisation of the governing partial differential equations using the FVM leads to sets of large sparse coefficient matrices. In this blog, we use Pointwise and OpenFOAM® to illustrate the effect of mesh renumbering on the matrix structure. In some circumstances, a poorly numbered mesh may result in solver divergence and failure of the simulation. Yet, not many realize that renumbering (ordering) of the cells in the Finite Volume Method (FVM) can affect the performance of the linear solver and thus the speed of the simulation. We all know that the mesh plays a vital role in CFD simulations.


 0 kommentar(er)
0 kommentar(er)
